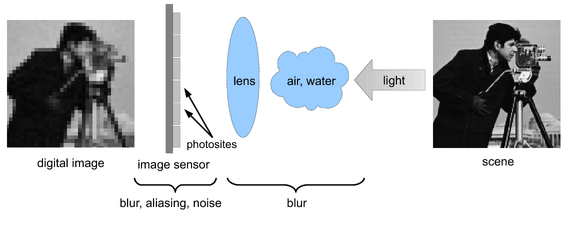
When designing and deploying computer vision systems, engineers are often confronted with the limits of available cameras with respect to the image quality they can provide. Similar to other sensing devices, cameras alter the measured signal and often yield images representing a degraded version of the original scene. Degradation sources include blur induced by such factors as the lens and sensors, frequency aliasing due to subsampling, signal quantization and circuitry reading noise.

To obtain higher camera resolution, one needs to increase the number of pixel sensors on the camera chip, which can be achieved by either reducing the size of the sensors or increasing the size of the chip. Unfortunately, the application of such solutions is limited due to constraints imposed by physics and image sensor technology. One such constraint is shot noise, which becomes more significant as the size of the pixel sensors decreases. Also, the higher level of capacitance associated with larger chips makes it difficult to accelerate the charge transfer rate in such structures. Finally, although high precision image sensors and optical components are sometimes available, they may also be prohibitively expensive for general purpose commercial applications.
Due to the previous limitations, there is a growing interest in image processing algorithms capable of overcoming the resolution limits of imaging systems. Super-resolution (SR) refers to techniques for synthesizing a HR image or video sequence from a set of degraded and aliased low-resolution (LR) ones. Generally, this is done by exploiting knowledge of the relative subpixel displacements of each LR image with respect to a reference frame. In situations where high quality vision systems cannot be incorporated or are too expensive to deploy, such algorithms may constitute an alternative and allow for the recovery of high quality images from more affordable imaging hardware.
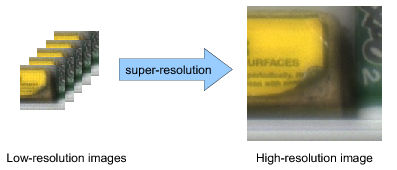
Super-resolution is generally formulated as an optimization problem, in which the HR image sought is computed by iteratively improving an initial solution until the desired level of convergence is achieved. The efficiency of the restoration process is determined by the convergence rate of the iterative method employed, which, in turn, depends on the SR problem formulation.

In this project, we are interested in the development of fast SR algorithms. The motivation comes from the fact that the computational complexity associated with many SR algorithms may hinder their use in time-critical applications. In particular, we developed an efficient method for accelerating computations associated with edge-preserving image SR problems in which a linear shift-invariant (LSI) point spread function (PSF) is employed. Our technique is suitable for SR scenarios where the motion between the observed LR images is translational. It is also possible to accelerate SR algorithms employing rational magnification factors. The use of such factors is motivated in part by the work of Lin and Shum suggesting that, under certain circumstances, optimal magnification factors for SR are non-integers.
The super-resolution literature is very rich and good summaries of existing methods are given by Borman and Stevenson and Park et al.. Special issues on super-resolution edited by Kang and Chaudhuri, Ng et al. and Hardie et al. were also published recently. Finally, different topics related to super-resolution, including motionless super-resolution, are discussed in two books by Chaudhuri.
To accelerate SR computations, some methods shift and interpolate all LR frames on a single HR grid, and then apply an iterative deblurring process to this temporary image in order to synthesize the HR image. However, the optimality of the HR images obtained in this manner is difficult to verify, since the interpolation process introduces errors in the input data. Nonetheless, when the motion model employed is translational, Elad and Hel-Or proposed a technique for fusing the LR images in a way that preserves the optimality of the SR reconstruction process in the maximum-likelihood sense. This optimality relies on the assumption that the translations between the LR frames are discretized on the HR grid. These authors assume that rounding the displacement values has a negligible effect on image quality, since it occurs on the HR grid. Farsiu et al. later adapted this method to the robust SR case. Tanaka and Okutomi also exploited such a discretization of the displacements between the observed pixels in order to accelerate computations in SR problems. Their method groups LR pixels whose positions are the same after discretization and computes the average of the pixel values in each group. The computations are then performed on this reduced set of averaged values instead of the original data.
However, such discretizations can produce undesirable artifacts in the restored HR image, particularly when small magnification factors are employed. Unlike these techniques, the proposed method does not sacrifice the optimality of the SR problem formulation when noninteger displacements are present between the LR images. When both the computational speed and the observation model accuracy are deemed important, our method thus constitutes a valuable approach.
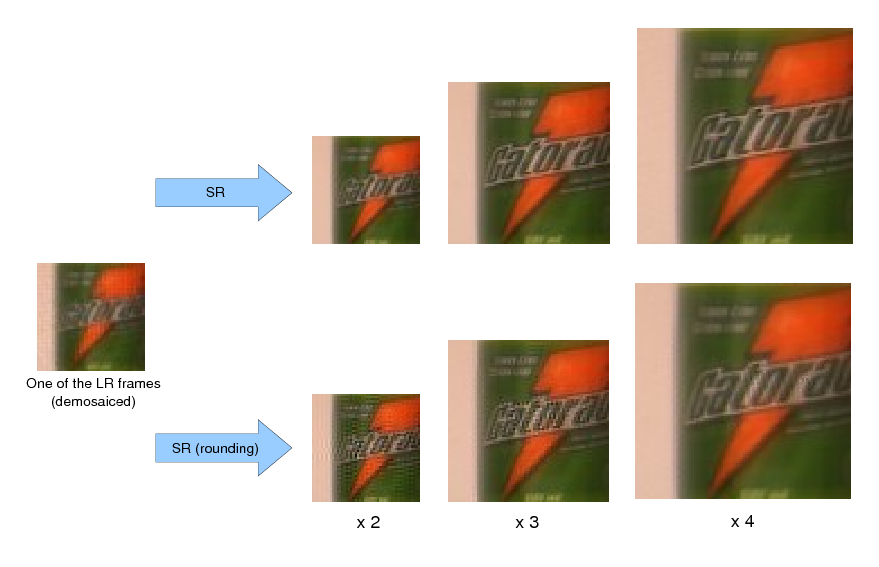
We conduct a few restoration experiments using a set of 235 Bayer CFA images captured with a Point Grey Flea2 digital camera. During video acquisition, the camera is slightly rotated manually about its vertical and horizontal axes, which results in small translational motion between the LR frames. The resolution of this set of images is increased using magnification factors of two, three and four, as shown below.

Magnification factor of two
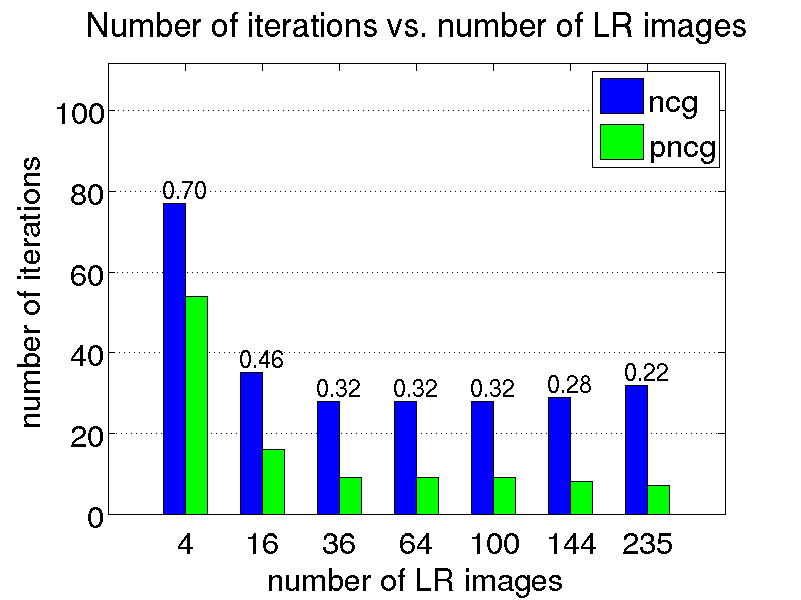
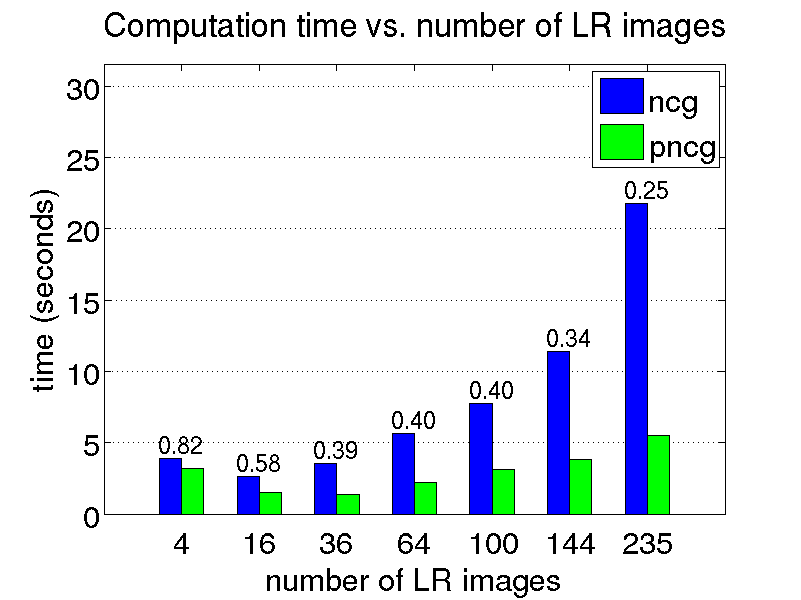
Magnification factor of three
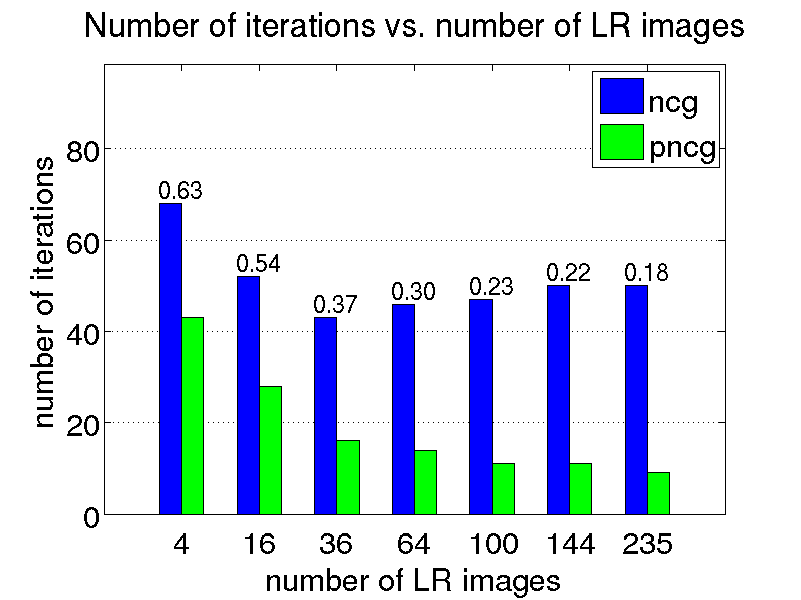
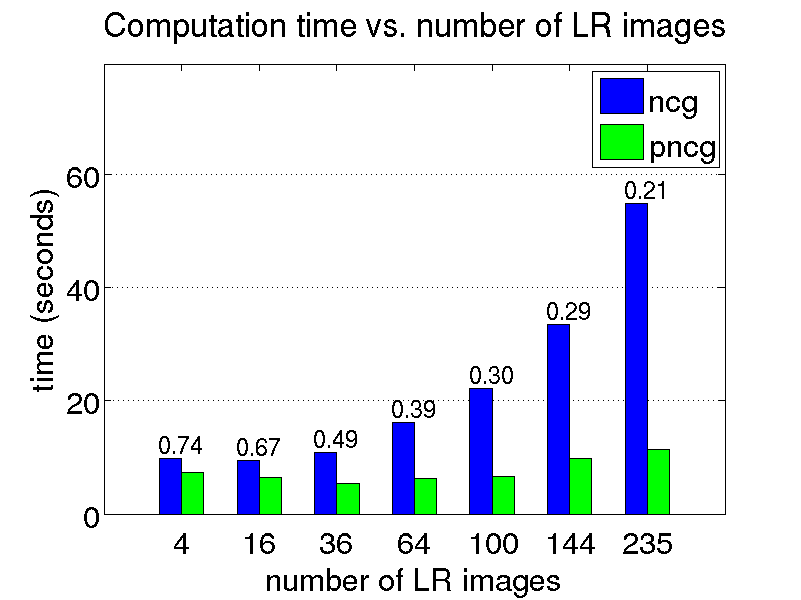
Magnification factor of four
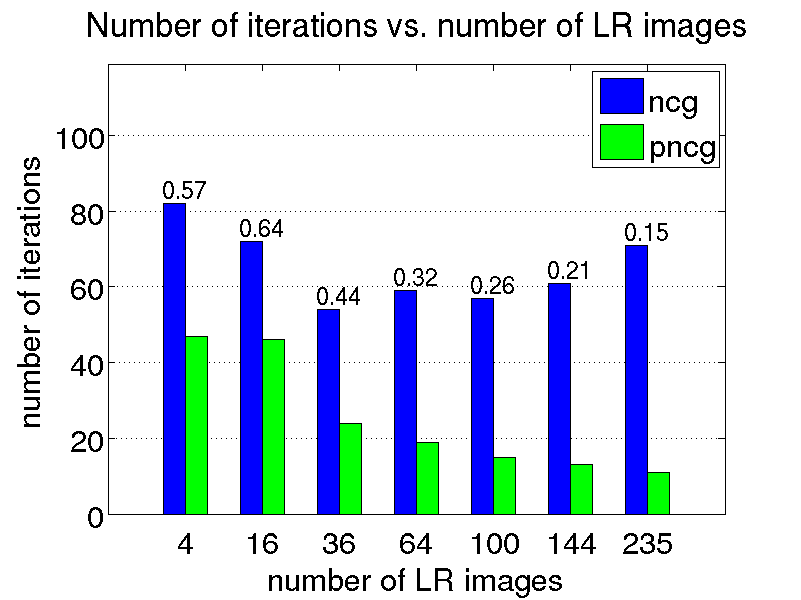
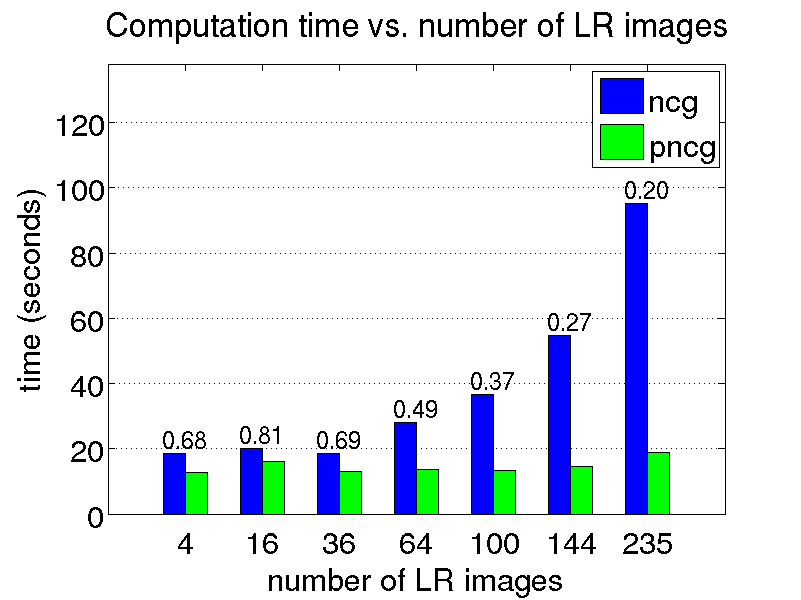

Last update: 5 November 2009